最小有向全域木を求める | Chu-Liu/Edmonds' algorithm

これはなに

最小全域木問題の有向グラフバージョン。

無向グラフに対する最小全域木は、クラスカル法とかプリム法とかで求められるけど、有向グラフの場合はどうすればいいのか気になったので調べてみた。

Chu-Liu/Edmonds' algorithmというアルゴリズムで計算量は $O(nm)$ 。頑張ったら $O(m\log n)$ や $O(m + n\log n)$ とかにできるらしい。 $O(m + n\log n)$ のやつはフィボナッチヒープを使うとのこと。

この記事では $O(nm)$ のアルゴリズムについてまとめる。

アルゴリズムとその証明

以下

$G=(V, E)$ ：単純有向グラフ
$c: E\rightarrow \mathbb{R}$ ：コスト関数
$r \in V$

とする。

また、誤解を与えないためにパスに関する包含関係の記号を次のように定義する。

パス $P= \left( \left( v_0, v_1 \right), \left( v_1, v_2 \right), \cdots \left( v_{k - 1}, v_k \right) \right) = v_0 v_1 \cdots v_k$ について

$(u, w)\in P$ $\Leftrightarrow$ $P$ に辺 $(u, w)$ が含まれる
$u \Subset P$ $\Leftrightarrow$ $\left(^\exists (w_1, w_2)\in P \text{ s.t. } w_1=u \lor w_2=u \right)$ $\Leftrightarrow$ $P$ に頂点 $u$ が含まれる *1
$\in$ 、 $\Subset$ の否定をそれぞれ $\notin$ 、 $\not\Subset$

とする。

Def.1 有向全域木

\begin{align} ^\forall v \in V-\{r\}, ^{\exists !}P\subset F: r\text{-}v\text{パス} \end{align} を満たす $G$ の部分グラフ $T=(V, F)$ を（ $G$ の $r$ に関する）有向全域木（spanning arborescence）という。ここで $r\text{-}v\text{パス}$ とは、 $r$ を始点、 $v$ を終点としたパスを意味する。

Def.2 最小有向全域木

$G$ の有向全域木 $T=(V, F)$ のうち、 $\displaystyle \sum_{e\in F}c(e)$ が最小となる $T$ を（ $G$ の $r$ に関する）最小有向全域木という。

Prop.3 有向全域木の存在性

$G$ が $r$ に関する有向全域木 $T=(V, F)$ をもつ $\Leftrightarrow$ $^\forall v \in V-\{r\}, ^\exists P\subset E: r\text{-}v\text{パス}$

proof

（ $\Rightarrow$ を示す）有向全域木の定義(Def.1)と $F\subset E$ より明らか。
（ $\Leftarrow$ を示す） $r$ に関する幅優先探索木が構成でき、これがちょうど有向全域木となる $_\blacksquare$

以下、 $G$ は有向全域木を持つと仮定する。
さらに $G$ の有向全域木は有限個なので最小有向全域木の存在性も仮定された。

E.g.

f:id:ark4rk:20170914232340p:plain

左から1番目のグラフを $G$ とすると

2番目のグラフは、 $G$ の $r$ に関する有向全域木であるが最小有向全域木ではない。コストは $19$ 。
3番目のグラフは、 $G$ の $r$ に関する有向全域木かつ最小有向全域木である。コストは $10$ 。
4番目のグラフは、 $r\text{-}b$ パスが複数あるため $G$ の有向全域木ではない。

Def.4 最小有向全域木問題

最小有向木全域問題を以下で形式化する。

\begin{align} \text{Input: }& G=(V, E): \text{単純有向グラフ}\\ & c: E\rightarrow \mathbb{R}: \text{コスト関数}\\ & r \in V\\ \\ \text{Output: }& T=(V, F): r\text{に関する最小有向全域木}\\ &\text{または}\displaystyle \sum_{e\in F}c(e) \end{align}

これを解くアルゴリズムを議論する前に、有向全域木に関する性質についてから議論する。

Prop.5

$T=(V, F)$ を $G$ の部分グラフとする。このとき

\begin{align} & T \text{ が}r\text{に関する有向全域木} \Leftrightarrow{} (\\ &\hspace{2em} T \text{ は有向閉路をもたない } \land \\ &\hspace{2em} ^\forall v \in V-\{r\}, ^{\exists !}u\in V \text{ s.t. } (u, v)\in F\\ &) \end{align}

が成り立つ。

proof

有向全域木の定義(Def.1)と $G$ が単純グラフ・有限グラフであることから示せる $_\blacksquare$

Def.6 $f_T$

$T=(V, F)$ を $G$ の $r$ に関する有向全域木とする。このときProp.5より \begin{align} V-\{r\}\ni v \mapsto (u, v) \in F \end{align} となる全単射が一意に存在する。有向全域木 $T$ によって定まるこの写像を $f_T$ と定義する。

Def.7 $T^* = (V, F^*)$

$v \in V - \{r\}$ に対して $\displaystyle c \left(\left(u, v\right)\right) = \min_{(w, v)\in E} c \left(\left(w, v\right)\right)$ を満たす $(u, v)\in E$ を選んで（複数ある場合は任意に一つ選ぶ）できる辺集合を $F^*$ とおく（つまり、 $|V| - 1=|F^*|$ を満たす）。

また、 $T^* := (V, F^*)$ とおく。

Prop.8

\begin{align} T^* \text{ が } G \text{ の有向全域木 } \Leftrightarrow T^* \text{ が } G \text{ の最小有向全域木} \end{align}

proof

（ $\Rightarrow$ を示す）
$T^*=(V, F^*)$ が有向全域木なので、 $f_{T^*}$ が定まる(Def.6)。ここで、 $^\forall T=(V, F): \text{有向全域木 }\,$ をとって固定する。 $F^*$ の定義より \begin{align} ^\forall v\in V - \{r\}, c \left(f_{T^*}\left( v \right)\right) \leq c \left(f_T\left( v \right)\right) \end{align} が成り立つ。よって \begin{align} \sum_{e\in F^*} c \left(e\right) = \sum_{ v \in V - \{r\} } c \left( f_{T^*} \left( v \right) \right) \leq \sum_{ v \in V - \{r\} } c \left( f_T \left( v \right) \right) = \sum_{e\in F} c \left(e\right) \end{align} が成り立つ。したがって $T^*$ は $G$ の最小有向全域木である。

（ $\Leftarrow$ を示す）
定義(Def.1, Def.2)より明らか $_\blacksquare$

Prop.9

\begin{align} &T^* \text{ が } G \text{ の有向全域木}\textbf{でない } \Leftrightarrow \\ &T^* \text{ には } r\not\Subset C \text{ となる有向閉路 }C\text{ が存在する} \end{align}

proof

（ $\Rightarrow$ を示す）
$F^*$ の定義より \begin{align} ^\forall v \in V-\{r\}, ^{\exists !}u\in V \text{ s.t. } (u, v)\in F^* \end{align} を満たし、また、 $T^*$ は有向全域木ではない。よってProp.5より $T^*$ には有向閉路 $C$ が存在する。さらに $F^*$ の定義より $^\forall v \in V , (v, r)\notin F^*$ が成り立つ。したがって、 $r\not\Subset C$ となる。

（ $\Leftarrow$ を示す）
$^\forall v \Subset C$ をとって固定する（これは $|C|>0$ より存在する）。

$^\exists P\subset F^*: r\text{-}v\text{パス }\,$ と仮定すると、 $^\forall u \in V-\{r\}$ について $(w, u)\in F^*$ となる $w$ はただひとつしか存在しないので $r\Subset C$ となる。これは $r\not\Subset C$ に矛盾する。よって $r\text{-}v$ パスは存在しない。したがって $T^*=(V, F^*)$ は有向全域木でない $_\blacksquare$

Prop.10

\begin{align} &T^* \text{ に }r\not\Subset C \text{ となる有向閉路が存在する} \Rightarrow \\ &^\exists T=(V, F): \text{最小有向全域木},\, ^\exists v_0 \Subset C \\ &\text{ s.t. } \left( f_T(v_0) \notin C \land\, ^\forall v\Subset C, v\neq v_0 \Rightarrow f_T(v)\in C\right) \end{align}

proof

$^\forall T=(V, F): \text{最小有向全域木}$ をとって固定する。

Prop.5より $T$ には有向閉路が存在しないので \begin{align} ^\exists v_0 \Subset C \text{ s.t. } f_T(v_0) \notin C \end{align} が成り立つ。ここで

$F' := \{f_T(v_0)\} \cup \{(u, v)\in C \mid v\neq v_0\} \cup \{(u, v)\in F \mid v\not\Subset C\}$
$T' := (V, F')$

と定めると、 $T'$ は有向全域木である（ $F$ から $F'$ へのパスの変化に注目すると、有向全域木であることが示せる）。

$^\forall v\in V-\{r\}$ について

のとき
- $c(f_{T'}(v)) \leq c(f_T(v))$ （ $\because f_{T'}(v) \in F^*$ ）
それ以外のとき
- $c(f_{T'}(v)) = c(f_T(v))$ （ $\because f_{T'}(v) = f_T(v)$ ）

が成り立つ。よって \begin{align} \sum_{e\in F'} c \left(e\right) = \sum_{ v \in V - \{r\} } c \left( f_{T'} \left( v \right) \right) \leq \sum_{ v \in V - \{r\} } c \left( f_T \left( v \right) \right) = \sum_{e\in F} c \left(e\right) \end{align} が成り立つ。さらに $T$ は最小有向全域木だったので \begin{align} \sum_{e\in F'} c \left(e\right) = \sum_{e\in F} c \left(e\right) \end{align} となる。したがって $T'$ も最小有向全域木である。

よって題意を満たす最小有向全域木 $T'$ が構成できた $_\blacksquare$

Prop.11

$v_0 \in V-\{r\}$
$\alpha \in \mathbb{R}$
$c': E\rightarrow \mathbb{R}$ \begin{align}c'\left(\left(u, v\right)\right) = \begin{cases} c\left(\left(u, v\right)\right) & v\neq v_0 \\ c\left(\left(u, v\right)\right) - \alpha & v = v_0 \end{cases}\end{align}
$T=(V, F): G\text{の部分グラフ}$

とする。このとき \begin{align} &T \text{ が }c\text{ における最小有向全域木 } \Leftrightarrow \\ &T\text{ が }c'\text{ における最小有向全域木 } \end{align} が成り立つ。

proof

（ $\Rightarrow$ を示す）
$T$ が $c$ における最小有向全域木だとする。

$^\forall T'=(V, F'): G\text{の有向全域木 }\,$ をとって固定する。

最小有向全域木の定義(Def.2)より \begin{align} \sum_{e\in F} c(e) \leq \sum_{e\in F'} c(e) \end{align} が成り立つ。つまり \begin{align} \sum_{v\in V-\{r\}}c\left(f_T\left(v\right)\right) \leq \sum_{v\in V-\{r\}}c\left(f_{T'}\left(v\right)\right) \end{align} が成り立つ。 $v_0 \in V-\{r\}$ と $c'$ の定義より \begin{align} \sum_{v\in V-\{r\}}c'\left(f_T\left(v\right)\right) &= \left( \sum_{v\in V-\{r\}}c\left(f_T\left(v\right)\right) \right) - \alpha \\ \sum_{v\in V-\{r\}}c'\left(f_{T'}\left(v\right)\right) &= \left( \sum_{v\in V-\{r\}}c\left(f_{T'}\left(v\right)\right) \right) - \alpha \end{align} となる。したがって \begin{align} \sum_{v\in V-\{r\}}c'\left(f_T\left(v\right)\right) \leq \sum_{v\in V-\{r\}}c'\left(f_{T'}\left(v\right)\right) \end{align} つまり \begin{align} \sum_{e\in F} c'(e) \leq \sum_{e\in F'} c'(e) \end{align} が成り立つ。したがって、 $T$ は $c'$ における最小有向全域木である。

（ $\Leftarrow$ を示す）
$\Rightarrow$ のときと同様にして成り立つ $_\blacksquare$

以上の議論から次のアルゴリズムが考えられる。

Chu-Liu/Edmonds' algorithm

\begin{align} \text{Input: }& G=(V, E): \text{単純有向グラフ}\\ & c: E\rightarrow \mathbb{R}: \text{コスト関数}\\ & r \in V\\ \\ \text{Output: }& T=(V, F): r\text{に関する最小有向全域木} \end{align}

Chu-Liu/Edmonds $(G=(V, E), c, r)$

$T^* = (V, F^*)$ を構成する。 $\cdots (1)$
If $^\exists C \subset F^* : \text{有向閉路 }\,$ $\cdots (2)$
　　 $C$ 上のコストを修正し $c_0$ とする。 $\cdots (3)$
　　 $C$ を1つのスーパーノードに縮約してグラフ $G'=(V', E')$ とコスト関数 $c'$ を構成する。 $\cdots (4)$
　　 $T'=(V', F') \leftarrow \text{Chu-Liu/Edmonds}(G', c', r)\,\,$ $\cdots (5)$
　　 $T'$ に $C$ の辺を、1本を除いてすべて加えることで $G$ の有向全域木 $(V, F)$ に拡張する。 $\cdots (6)$
　　 $(V, F)$ を返す。
Else
　　 $(V, F^*)$ を返す。 $\cdots (7)$
Endif

操作の詳細

各操作を詳しく書くと次のようになる。

(1)

Def.7で定義されている $T^* = (V, F^*)$ を構成する。

(2)

$T^* = (V, F^*)$ に有向閉路があるかを判定する。発見した場合、その有向閉路を $C$ とする。

(3)

$c_0: E\rightarrow \mathbb{R}$ を次のように構成する。

\begin{align} c_0\left(\left(u, v\right)\right) = \begin{cases}\displaystyle c\left(\left(u, v\right)\right) - \min_{(u, v)\in E}c\left(\left(u, v\right)\right) & v\Subset C \\ c\left(\left(u, v\right)\right) & v\not\Subset C \end{cases} \end{align}

(4)

$V$ 、 $E$ 、 $c_0: E\rightarrow \mathbb{R}$ から、有向閉路 $C$ をスーパーノードとして縮約したグラフとコスト関数 $c'$ をつくる。具体的には次のように構成する。

$V' = \{v\in V \mid v\not\Subset C\} \cup \{C\}$
\begin{align} E' &= \{(u, v)\in E \mid u, v\not\Subset C\}\\ &\cup \{(u, C) \mid ^\exists v \Subset C \text{ s.t. } (u, v) \in E \land u\not\Subset C \}\\ &\cup \{(C, v) \mid ^\exists u \Subset C \text{ s.t. } (u, v) \in E \land v\not\Subset C \} \end{align}
\begin{align} c'\left(\left(u, v\right)\right) = \begin{cases} c_0\left(\left(u, v\right)\right) & u \neq C \land v\neq C \\ \min \{ c_0\left(\left(u, w\right)\right) \mid (u, w)\in E \} & v = C \\ \min \{ c_0\left(\left(w, v\right)\right) \mid (w, v)\in E \} & u = C \end{cases} \end{align}

(5)

Chu-Liu/Edmonds $(G', c', r)$ で得た $G'$ の最小有向木を $T'=(V', F')$ とする。

(6)

$T'=(V', F')$ において $e' = (u, C)\in F'$ となる辺 $e$ を見つける。 (4)においてグラフを縮約したときに $e'$ のもととなった辺を $e = (u, v)$ とする（つまり、 $v\Subset C$ を満たす）。

$F$ を次のように構成して、 $(V', F')$ を $(V, F)$ に拡張する。 \begin{align} F = (F'-\{e'\}) \cup \{e\} \cup \{(w_1, w_2) \in C \mid w_2 \neq v \} \end{align}

アルゴリズムの正当性

Prop.8, 9により、「 $(V, F^*)$ に有向閉路が存在しないならば $(V, F^*)$ が最小有向全域木である」ことがわかる。有向閉路 $C$ が見つからなかった場合は、 $(V, F^*)$ をそのまま返してよい（操作(7)）。

次に、有向閉路 $C$ が見つかった場合について考える。

操作(3)でコスト関数を修正するが、Prop.11により修正後に得られる最小有向全域木に変化しないことが保証される。なお、Prop.11における $\alpha$ は $\min_{(u, v)\in E}c\left(\left(u, v\right)\right)$ に対応する。

Prop.10より、 $C$ に入る辺 $e\in E$ がちょうど1本と、 $C$ 上の辺がちょうど $|C| - 1$ 本もつような辺集合 $F_0$ が存在して、 $(V, F_0)$ が $G$ の最小有向全域木となる。

さらに、修正後のコスト関数 $c_0$ に関して有向閉路 $C$ 上の辺のコストはすべて $0$ である。よって、この $C$ 上の頂点は同一視できる。よって $C$ を一つの頂点として縮約したグラフ $(V', E')$ 上から最小有向全域木を見つけたのち、縮約した部分を元に拡張すれば、最終的に欲しかった $G$ の最小有向全域木が手に入る。（操作(4),(5),(6)）

アルゴリズムの計算量

$n := |V|$ 、 $m := |E|$ とする。

(5)で再帰して計算をするが、縮約するたびに頂点数が少なくとも $1$ だけ減るので、再帰の回数は $O(n)$ 。また、(1),(2),(3),(4),(6)の操作はすべて $O(n + m)$ で計算できる。

よって、このアルゴリズム全体の計算量は $O\left(n\left(n+m\right)\right) = O(nm)$ となる。

アルゴリズムの挙動の例

f:id:ark4rk:20170915004537p:plain

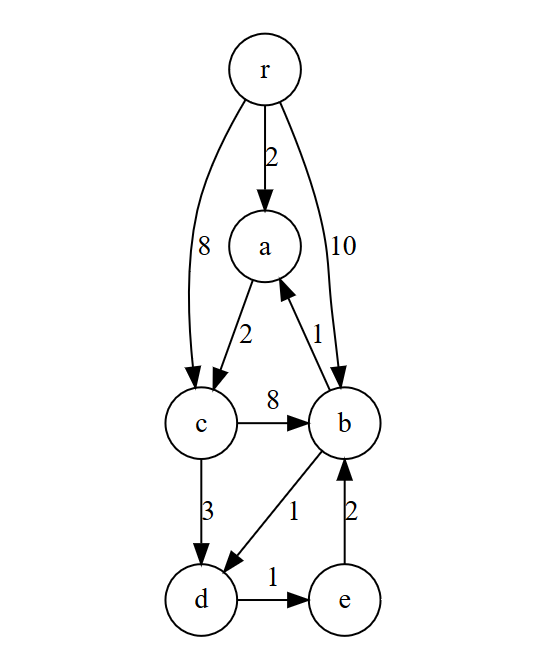
これをグラフ $G=(V, E)$ とし、 $r\in V$ とコスト関数 $c$ も図に従うとする。
この最小有向全域木を求めたい。

f:id:ark4rk:20170915004553p:plain

$T^* =(V, F^*)$ を構成する(操作(1))。
また、有向閉路 $C = \left(\left(b, d\right), \left(d, e\right), \left(e, v\right)\right)$ が検出できる(操作(2))。

f:id:ark4rk:20170915004619p:plain

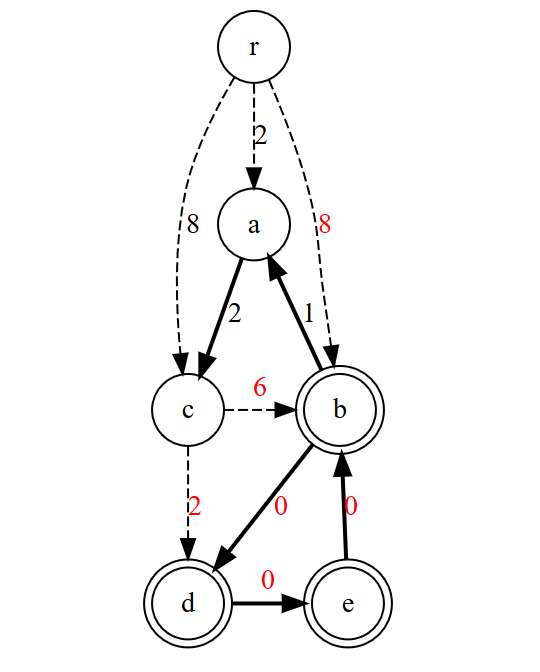
有向閉路 $C$ に入る各辺のコストを修正する(操作(3))。(赤字が修正箇所)

f:id:ark4rk:20170915004623p:plain

$C$ に関して縮約したグラフ $G'=(V', E')$ とコスト関数 $c'$ を構成する(操作(4))。
次に、この縮約したグラフに関して再帰的に最小有向全域木を求める(操作(5))。
- ただし、名前が被ってしまうので説明の都合上、グラフ $G^{(1)}=(V^{(1)}, E^{(1)})$ 、コスト関数 $c^{(1)}$ とする。

f:id:ark4rk:20170915004701p:plain

$T^{(1)*} =(V^{(1)}, F^{(1)*})$ を構成する(操作(1))。
また、有向閉路 $C^{(1)} = \left(\left(a, c\right), \left(c, \{b, d, e\} \right), \left(\{b, d, e\}, a\right)\right)$ が検出できる(操作(2))。

f:id:ark4rk:20170915004712p:plain

有向閉路 $C^{(1)}$ に入る各辺のコストを修正する(操作(3))。(赤字が修正箇所)

f:id:ark4rk:20170915004719p:plain

$C^{(1)}$ に関して縮約したグラフとそのコスト関数を構成する(操作(4))。
次に、この縮約したグラフに関して再帰的に最小有向全域木を求める(操作(5))。
- 説明の都合上、グラフ $G^{(2)}=(V^{(2)}, E^{(2)})$ 、コスト関数 $c^{(2)}$ とする。

f:id:ark4rk:20170915004727p:plain

$T^{(2)*} =(V^{(2)}, F^{(2)*})$ を構成する(操作(1))。
有向閉路が検出できない(操作(2))ため、 $(V^{(2)}, F^{(2)*})$ を $G^{(2)}$ の最小有向全域木として返す(操作(7))。

f:id:ark4rk:20170915004736p:plain

得られた $G^{(2)}$ の最小有向全域木からグラフを拡張して $G^{(1)}$ の最小有向全域木を構成する(操作(6))。
できた $G^{(1)}$ の最小有向全域木を返す。

f:id:ark4rk:20170915004744p:plain

得られた $G^{(1)}$ の最小有向全域木からグラフを拡張して $G$ の最小有向全域木を構成する(操作(6))。
できた $G$ の最小有向全域木を返す。

f:id:ark4rk:20170915004752p:plain

得られた最小有向全域木と元のコスト関数を表示するとこのようになる。
無事、最小有向全域木は求められ、さらに最小コストは $10$ であることがわかる。

実装

実際にD言語で実装してみた。

import std.range;
import std.algorithm;
import std.container : DList;

// Chu-Liu/Edmonds' algorithm
//   最小有向全域木を求める

class ChuLiuEdmonds(T) {

private:
    size_t _size;
    Vertex[] _vertices;
    Vertex _root;

public:
    this(size_t size, size_t rootIndex) {
        _size = size;
        _vertices = size.iota.map!(i => new Vertex(i)).array;
        _root = _vertices[rootIndex];
    }

    void addEdge(size_t startIndex, size_t endIndex, T weight) {
        if (endIndex == _root.index) return; // rootに入る辺は除外する（最小木に含まれる可能性がないため）
        if (startIndex == endIndex) return; // 自己ループは除外する
        Vertex start = _vertices[startIndex];
        Vertex end   = _vertices[endIndex];
        end.edges ~= Edge(start, end, weight);
    }

    // O(V(V + E)) = O(VE)
    T solve() {
        foreach(v; _vertices) {
            v.onCycle = false;
            v.isVisited = false;
            if (!v.hasEdge) continue;
            v.minEdge = v.edges.minElement!"a.weight";
        }

        // v を含む閉路を縮約したグラフの最小コストを返す
        T rec(Vertex v) {
            auto sub = new ChuLiuEdmonds!T(_size, _root.index);
            auto getIndex  = (Vertex u) => u.onCycle ? v.index : u.index;
            foreach(u; _vertices) {
                foreach(e; u.edges) {
                    sub.addEdge(
                        getIndex(e.start),
                        getIndex(e.end),
                        e.weight - (u.onCycle ? u.minEdge.weight : 0)
                    );
                }
            }
            return sub.solve;
        }

        // 閉路検出
        auto list = DList!Vertex();
        size_t[] cnt = new size_t[_size];
        foreach(v; _vertices) {
            if (v.hasEdge) cnt[v.minEdge.start.index]++;
        }
        foreach(i, c; cnt) {
            if (c==0) list.insertBack(_vertices[i]);
        }
        while(!list.empty) {
            Vertex v = list.front;
            list.removeFront;
            if (v.hasEdge) {
                size_t i = v.minEdge.start.index;
                if (--cnt[i]==0) {
                    list.insertBack(_vertices[i]);
                }
            }
        }
        foreach(i, c; cnt) {
            if (c > 0) {
                // 閉路が検出された
                Vertex v = _vertices[i];
                Vertex u = v;
                do {
                    u.onCycle = true;
                    u = u.minEdge.start;
                } while(u !is v);
                return rec(v) + _vertices.filter!"a.onCycle".map!"a.minEdge.weight".sum;
            }
        }

        // 閉路が検出されなかったとき
        return _vertices.filter!"a.hasEdge".map!"a.minEdge.weight".sum;
    }

private:
    class Vertex {
        size_t index;
        Edge[] edges; // assert(edges.all!(e => e.end is this))
        Edge minEdge;
        bool onCycle;
        bool isVisited;
        this(size_t index) {
            this.index = index;
        }
        bool hasEdge() {
            return edges.length > 0;
        }
    }

    struct Edge {
        Vertex start, end;
        T weight;
    }

}

http://judge.u-aizu.ac.jp/onlinejudge/description.jsp?id=GRL_2_B&lang=jp

この問題でACが取れたことを確認した。

参考文献

www.kyoritsu-pub.co.jp https://www.maruzen-publishing.co.jp/item/b294196.htmlwww.maruzen-publishing.co.jp

*1: $\Subset$ の記号はここでは便宜上使っているだけで、一般的に使用されている記法ではないです。

Ark's Blog

引っ越しました→ https://blog.arkark.dev/

最小有向全域木を求める | Chu-Liu/Edmonds' algorithm

これはなに

アルゴリズムとその証明

Def.1 有向全域木

Def.2 最小有向全域木

Prop.3 有向全域木の存在性

proof

E.g.

Def.4 最小有向全域木問題

Prop.5

proof

Def.6 $f_T$

Def.7 $T^* = (V, F^*)$

Prop.8

proof

Prop.9

proof

Prop.10

proof

Prop.11

proof

Chu-Liu/Edmonds' algorithm

Chu-Liu/Edmonds $(G=(V, E), c, r)$

操作の詳細

(1)

(2)

(3)

(4)

(5)

(6)

アルゴリズムの正当性

アルゴリズムの計算量

アルゴリズムの挙動の例

実装

参考文献